오늘은 최단거리 구하는 알고리즘 중 다익스트라 알고리즘에 대해 알아보려 합니다.
학교에서 갓 2학년에 되었을 때 알고리즘 수업시간에 다익스트라를 배웠었는데요, 사실 1학년 말에도 과 학회 선배들이 다익스트라를 알려줬었습니다. 하지만 저는 이것만큼 거부감드는게 없었어요ㅠㅠ 그냥 다익스트라 라는 단어 자체가 너무 어려워 보였던 것 같습니다. 하지만 이제와서 다시보니 왜 이렇게 간단한 개념을 이해조차 못했는지.. 이렇게 보니 저도 그 때보다 성장하긴 했나봐요ㅎㅎ..
다익스트라는 V개의 정점과 음수가 아닌 E개의 간선을 가진 그래프 G에서 특정 출발 정점 (S) 에서부터 다른 모든 정점까지의 최단경로를 구하는 알고리즘 (1:N) 입니다.
벨만-포드 알고리즘과 달리 음의 가중치를 가지지 않아, 각 정점을 최대 한 번씩만 방문하여 최단 거리를 확정합니다. 아직 방문하지 않은 정점들 중 최단거리인 점을 찾아 방문하여 최단거리를 확정하고, 이를 반복하는 식으로 진행되기 때문에 시간 복잡도는 O(V*V)가 됩니다.
하지만 방문하지 않은 정점 중에서 최단 거리가 최소인 정점을 찾는 과정에서 Priority Queue / Heap 자료구조를 사용한다면 시간복잡도 O(V*logV)의 개선된 알고리즘을 구현할 수 있습니다.
그래서 저는 오늘 Priority Queue를 사용한 다익스트라 알고리즘을 구현해보려 합니다 :)
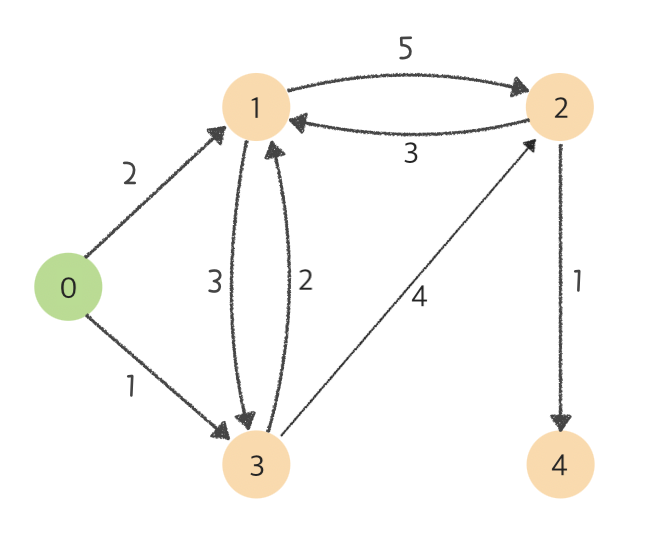
과정을 천천히 살펴보기 위해 아래와 같은 그래프를 예시로 사용해보겠습니다. 시작점은 0번 노드입니다.
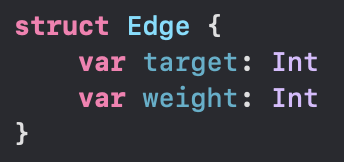
Initialize. 먼저 코드의 구현을 위해 그래프 정보와 max_value를 설정해주었습니다. 그리고 이후 사용을 위해 Edge라는 구조체를 생성해주었습니다.

Step 1. 시작점부터의 모든 거리를 무한으로 초기화 합니다. (시작점은 0)

Step 2. 시작점부터 Priority Queue에 넣어줍니다. 이 때, Priority Queue는 비용이 작은 순서대로 우선순위를 부여하도록 선언합니다.

Step 3. 이후 Priority Queue에 최단 거리에 해당하는 정보만 넣어 갱신하는 과정을 반복해줍니다.

위 과정을 시각화 한다면 아래와 같습니다.
아래 사진은 Priority Queue에서 pop 되는 순서대로 edge와 거리 배열을 출력한 것입니다.

'알고리즘 > 알고리즘&자료구조' 카테고리의 다른 글
| 인덱스 트리 (Indexed Tree) (0) | 2021.03.24 |
|---|---|
| 플로이드 와샬 (Floyd Warshall) (0) | 2021.03.23 |
| 벨만-포드 (Bellman-Ford) (0) | 2021.03.08 |
| 크루스칼 (Kruskal) (0) | 2021.03.04 |
| Disjoint-Set / Union-Find (디스조인트 셋, 유니온 파인드) (0) | 2021.03.03 |




댓글