구간합을 구하는 트리 종류에는 인덱스 트리, 세그먼트 트리, 펜윅 트리가 있습니다. 그 중에서도 오늘은 인덱스 트리(Indexed Tree) 에 대해 알아보려 합니다. 참고로, 인덱스 트리에 포함되어 있는 종류 중 하나가 세그먼트 트리이기 때문에 세그먼트 트리로 풀 수 있는 문제는 인덱스 트리로 모두 풀 수 있습니다.
인덱스 트리는 A라는 수열에서 구간 S ~ E 가 주어졌을 때, A의 구간 S ~ E 사이의 합을 구하기 위해 사용합니다. 중간 중간 A의 값이 하나씩 바뀔 때마다 그 구간의 합을 구할 때 인덱스 트리를 사용할 수 있습니다.
구현 과정을 보면 다소 복잡해 보일 수 있지만, 그래도 천천히 단계를 밟으면 쉽게 이해할 수 있습니다.
저는 Swift로 구현을 해볼건데요, 마지막에 Java 로 구현한 코드도 첨부하였습니다.
그럼 Indexed Tree를 구현해보겠습니다! :)
우리는 인덱스 트리를 { 1, 3, 4, 8, 10, 11, 12 } 이라는 배열에 적용해서 각 구간의 합을 알아볼거예요. 만약 이 배열로 인덱스 트리를 구성한다면 아래와 같은 트리를 만들게 될 것입니다.

그럼 이런 트리를 만들기 위한 초기화 과정을 먼저 만들어볼게요.
1️⃣IndexedTree라는 클래스를 만들어줍니다. 그리고 클래스의 initialize 단계에서 tree 배열을 초기화해줍니다.
이때, depth는 트리의 depth를 뜻하기 때문에 배열의 크기보다 크거나 같은 수 중 가장 작은 2^k 값에서의 k가 이 트리의 depth가 됩니다. 트리의 depth는 루트 노드에서 특정 노드까지 도달하는데 사용하는 간선의 개수 입니다. 예를 들면, 배열의 크기가 7일 때 배열의 크기보다 큰 수중 가장 작은 2^k 값은 2^3인 8입니다. 따라서 depth는 3이 됩니다.
leafSize는 해당 트리의 리프 노드의 개수를 말합니다. 리프노드의 개수는 당연하게도 2^depth가 되겠죠? 혹시 이해가 가지 않는다면 Tree의 용어나 특성을 먼저 공부하고 오셔야 해요!
그리고 leafSize가 8인 트리의 총 노드의 수는 2 * 8 - 1 개가 되는데요, 우리는 tree 배열의 0번째 인덱스를 사용하지 않기 때문에 tree 배열의 사이즈를 2^depth * 2 또는 2^(depth+1) 로 해줍니다. 2^depth * 2 나 2^(depth+1) 이나 같은말이예용

2️⃣이제 tree배열에 각 구간의 합을 넣어주는 makeTree 메서드를 구현합니다.
makeTree의 파라미터는 다음과 같습니다.
- index : 현재 값을 넣어주고 싶은 tree의 인덱스
- start : 값을 넣어주고 싶은 숫자 배열(values)의 start 인덱스
- end : 값을 넣어주고 싶은 숫자 배열(values)의 end 인덱스
즉, init 마지막에 makeTree를 실행하려면 makeTree(1, 0, values.count-1) 을 넣어줘야겠죠?

이제, 메서드 내용을 볼까요? start == end 일 경우, 검사하고 있는 구간이 숫자 배열(values) 중 하나를 바라보고 있다는 뜻입니다. 따라서 그 하나의 인덱스가 (value의 개수 - 1)보다 작다면, 즉 그 인덱스가 숫자 배열(values)의 유효한 인덱스라면 values[start]를 tree[index]에 넣어주죠.
이게 무슨 말이냐면, 위에 있는 그래프 이미지에서 구간이 7 ~ 7 일 경우, values의 범위를 벗어나는 인덱스에 해당하겠죠? 근데 우리가 가진 values 배열은 0 ~ 6의 구간에만 속합니다. 따라서 구간이 0 ~ 6 사이에 있어야 values에 있는 값을 넣어줄 수 있다는 거죠. 인덱스가 7인 노드는 values 배열에서 벗어난 구간이기 때문에 우리는 tree[index]에 0을 넣어줘야 합니다.
자, 그럼 start와 end가 같지 않다면? start ~ end 구간을 바라보고 있다. 이 말이겠죠?
그럼 이 구간을 start ~ mid와 mid+1 ~ end 구간으로 나누어서 다시 검사해줍니다. 재귀형태로 말이죠. 그럼 결국 가장 아래 리프노드부터 values의 값을 저장하고, 이후 부모 노드로 올라와서는 그 왼쪽 자식의 노드와 오른쪽 자식의 노드 값을 합한 값을 tree[index] 값이 저장하게 됩니다.
사실 말로 설명하려니 조금.. 복잡하고 어려운데요.... 직접 구현할 때 print 해가면서 확인하면 무슨 말인지 알거예요..ㅠㅠ
3️⃣드디어! 구간의 합을 조회해볼거예요!! 어떠한 구간의 합을 조회하는 query 메서드를 구현해보겠습니다.
query 메서드의 파라미터는 다음과 같습니다.
- index : 현재 바라보고 있는 tree의 인덱스
- start : 현재 바라보고 있는 구간의 start 인덱스
- end : 현재 바라보고 있는 구간의 end 인덱스
- queryStart : 구간 합을 구하고자 하는 구간의 start 인덱스
- queryEnd : 구간 합을 구하고자 하는 구간의 end 인덱스
여기서도 마찬가지로 재귀를 사용해서 구간 합을 구하게 됩니다.

검사하고자 하는 범위(qStart ~ qEnd)가 바라보고 있는 배열의 범위(start ~ end)를 벗어난 경우 0을 더해주고, 바라보고 있는 배열의 범위가 검사하고자 하는 범위에 포함되어 있다면 현재 tree의 index값을 더해주죠. tree[index]가 해당 구간의 합을 나타내고 있으니까요. 만약, 바라보고 있는 배열의 범위가 검사하고자 하는 범위에 걸쳐있다면? start ~ mid와 mid+1 ~ end로 나눠서 왼쪽 트리 + 오른쪽 트리 의 합으로 구하게 됩니다. 즉, 아래 이미지 처럼 바라보고 있는 범위(green)가 구간 합을 구하고자 하는 범위(pink)에 걸쳐 있다면 나누고 나눠서 구간 합을 구하게 되는거죠!

4️⃣마지막으로 value의 배열 중 하나의 값을 한 번 바꿔보겠습니다. 그러기 위해서는 구간 합 트리에 update를 해줘야 겠죠? update 메서드를 구현해봅시다.
update 메서드의 파라미터는 다음과 같습니다.
- index : 현재 바라보고 있는 tree의 인덱스
- start : 현재 바라보고 있는 구간의 start 인덱스
- end : 현재 바라보고 있는 구간의 end 인덱스
- valueIndex : 업데이트하려고 하는 요소의 숫자 배열(values) 에서의 인덱스
- diff : 업데이트하려고 하는 값과 원래 값의 차이 (만약 원래 3인 값을 1로 바꾸려고 한다면 diff는 -2가 되어야 합니다)

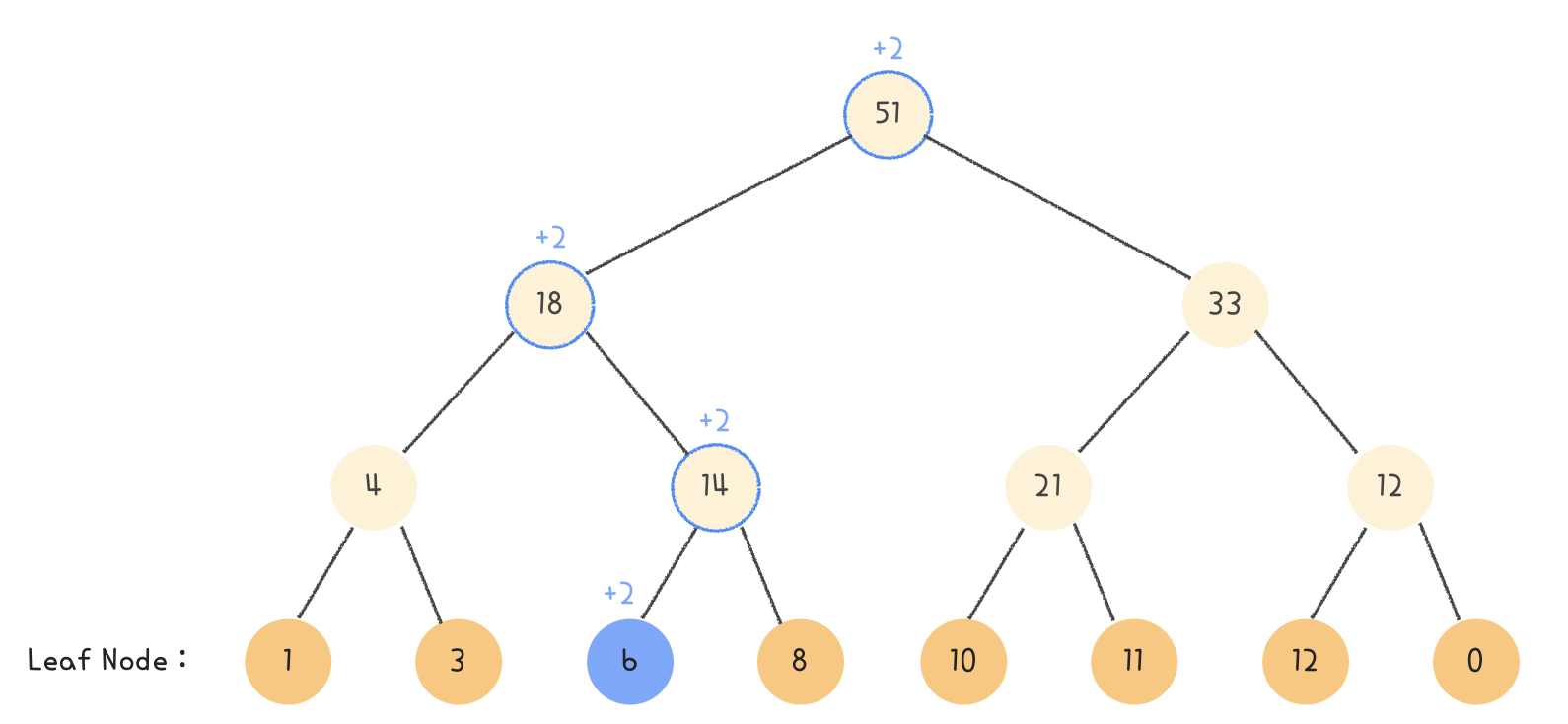
즉, 루트 노드부터 시작해서 update하려는 리프 노드까지 내려가며 diff 값을 더해줍니다. 아래 이미지처럼 말이죠!
아래 이미지는 update(1, 0, leafSize-1, 2, 2) 를 실행한 결과입니다.
지금까지 알고리즘 게시물 작성하면서 인덱스 트리만큼 말로 설명하기 힘들었던 적이 없었던 것 같아요.. 뭔가 옆에 딱 붙들어두고 제스쳐로 딱딱 가리키면서 설명하는게 훨씬 쉬울 것 같은데, 글로만 설명하려니 정말 복잡했습니다😂 언젠가 미래의 제가 인덱스 트리를 다시 공부하기 위해 이 게시물을 볼 때는 그래도 이해하기 쉬웠으면 좋겠네요ㅎㅎ 미래의 나 화이팅..❗️ㅋㅋㅋ
전체 코드는 아래를 보시면 됩니다. :)
👉Swift 구현 코드 보기
👉Java 구현 코드 보기
'알고리즘 > 알고리즘&자료구조' 카테고리의 다른 글
| LCA (Lowest Common Ancestor) (0) | 2021.04.01 |
|---|---|
| 확장 유클리드 호제법 (0) | 2021.03.25 |
| 플로이드 와샬 (Floyd Warshall) (0) | 2021.03.23 |
| 다익스트라 (Dijkstra) (0) | 2021.03.09 |
| 벨만-포드 (Bellman-Ford) (0) | 2021.03.08 |






댓글