오늘은 최단 경로를 찾는 대표적인 기법 중 하나인 벨만-포드 알고리즘을 알아보려 합니다. 벨만-포드는 V개의 정점과 E개의 간선을 가진 가중 그래프 G에서 특정 출발 정점 S 에서부터 다른 정점까지의 최단경로 (1:N) 를 구하는 알고리즘입니다.
다익스트라와 달리 음의 가중치를 가진 간선을 가질 수 있고, 때문에 음의 사이클의 존재 여부를 확인해주어야 합니다. 최단거리를 구하기 위해 최대 (V-1)번 E개의 모든 간선을 확인하고, 음의 사이클을 확인하기 위해 한 번 더 E개의 간선을 확인합니다. 따라서 벨만-포드 알고리즘은 O(VE)의 시간복잡도를 가지게 됩니다.
구체적인 벨만-포드 Swift 코드를 보기 전에, 벨만-포드 알고리즘의 구현을 슈도 코드(Pseudo Code)로 먼저 보겠습니다.

슈도 코드만 처음 접할 때 이해가 가지 않으실까봐 제가 부연설명을 조금 달아놓긴 했는데... 사실 그냥 슈도코드 자체만으로도 머리가 복잡해질 수 있어요.. 저도 처음엔 그랬거든요ㅎㅅㅎ
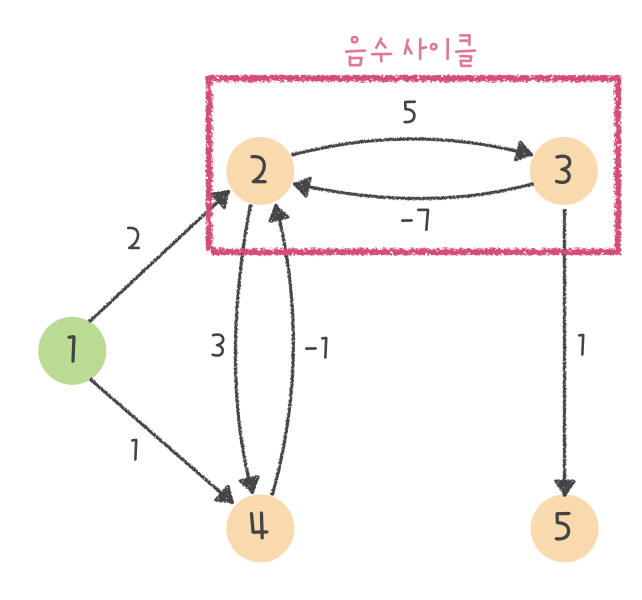
그래서 다음 그래프를 예시로 들어서 구체적으로 단계를 밟아보려 합니다. 아래 그래프의 정점 개수(V)는 5개이며, 시작 정점은 1 입니다.

그리고 저는 간선의 정보를 Bus라는 구조체로 저장하도록 하였습니다.

그럼 벨만-포드 알고리즘의 구현 단계를 천천히 밟아볼까요?
Step 1. 시작 정점부터 다른 정점까지의 거리 값을 무한으로 초기화합니다. (시작 정점은 0)


Step 2. 현재 정점의 모든 인접 정점들을 탐색하여 기존에 기록된 인접 정점까지의 거리보다 현재 정점을 거쳐 인접 정점에 도달하는 거리가 더 짧다면 인접 정점까지의 거리를 갱신합니다. -> 즉 간단히 말하면, 정점개수(V)-1 만큼 반복해서 모든 간선 E개를 모두 체크해줍니다. O((V-1)|E|)


그럼 아래와 같은 과정을 반복하게 됩니다. (아래 그림은 1번 반복한 과정을 보여줍니다. 이런 과정을 V-1번이나 하게 되는거죠!)


Step 4. 그럼 마지막으로 음수 사이클의 여부를 확인하기 위해 모든 간선 E개를 한 번 더 체크 해줍니다. 그리고 이 과정에서 거리가 한 번 더 갱신되는 경우가 생긴다면?? 바로 음수 사이클이 있다는 소리가 되죠. 그리고 제가 예시로 든 그래프는 아래와 같은 음수 사이클이 발생하게 됩니다 :)

따라서 위에서 보여드렸던 슈도 코드를 Swift 코드로 바꿔보면 아래와 같은 코드를 볼 수 있습니다!

'알고리즘 > 알고리즘&자료구조' 카테고리의 다른 글
| 플로이드 와샬 (Floyd Warshall) (0) | 2021.03.23 |
|---|---|
| 다익스트라 (Dijkstra) (0) | 2021.03.09 |
| 크루스칼 (Kruskal) (0) | 2021.03.04 |
| Disjoint-Set / Union-Find (디스조인트 셋, 유니온 파인드) (0) | 2021.03.03 |
| Lower / Upper Bound (0) | 2021.02.26 |




댓글