ㅎ..제가 말이죠.. 요즘 Swift로 알고리즘을 풀어보려고 연습중인데, 거의 없는게 없는 Java로 알고리즘 문제를 풀다가 Swift로 풀려고 하니 없는게 너어무 많더라구요??? Stack도 Queue도 PriorityQueue도?!?
구글링 해보니 직접구현해야하는 거 같더라구요??ㅋㅋㅋㅋㅋ
예. 근데 이것도 사실 이 게시물 작성했을 당시에 iOS / Swift 공부를 한지 겨우 2개월밖에 안됐을 때라 그랬나봐용.. stack 은 그냥 배열에서 removeLast( ) 사용해서 stack처럼 사용하면 되구.. queue는 그냥 배열에서 removeFirst( ), removeLast( ) 사용해서 queue처럼 사용하면 되구.. PriorityQueue도 .sorted(by: { Bool }) 이런식으로 해서 정렬을 하면 되었더랍니당...하하 그치만 그래도 이번 기회에 Heap 공부를 했으니 만족합니다!!
허흐ㅠㅠ Java 사용할 때 Priority Queue 정말 많이 사용했는데..
그래서 이번에는 Priority Queue를 Swift로 직접 구현해보기 위해, Priority Queue에서 사용되는 Heap 자료구조를 정리했습니다!!
예전에 학교에서 자료구조 수업을 들을 때는 Heap이 복잡하다고 생각했었는데, 막상 지금 다시보니 엄청 간단한 자료구조였더라구요?(그땐 그냥 공부가 하기 싫었나봐요) 그래서 간단하게 정리했습니다!
Heap이란?
여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조 입니다. 나중에 보면 아시겠지만, 추가적인 메모리를 잡아먹지도 않습니다. 그리고 삽입/삭제 과정이 부모노드와 자식노드 간의 비교를 통해 이루어지기 때문에 삽입과 삭제에 걸리는 시간이 O(log n)을 나타낼 정도로 빠릅니다. 그래서 Heap Sort (힙 정렬)의 시간복잡도도 O(n log n)이 되죠.
힙(Heap) 자료구조는 최대 힙(max heap)과 최소 힙(min heap)으로 나뉩니다.
- 최대 힙(max heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리를 구성합니다.
- 최소 힙(min heap) : 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리를 구성합니다.

그리고 원래 이진 탐색 트리에서 중복된 값을 허용하지 않는 것과 다르게, Heap Tree (힙 트리) 에서는 중복된 값을 허용합니다. 이 게시물에서는 Int타입의 최대 힙(max heap)을 기준으로 설명하겠습니다.
Heap의 구현
힙(Heap)을 구성하는 표준적인 자료구조는 배열 입니다. 구현을 쉽게 하기 위해서 배열의 첫 번째 index인 0은 사용하지 않습니다.
var heap: [Int] = [-1,9,7,6,5,4,3,2,2,1,3]
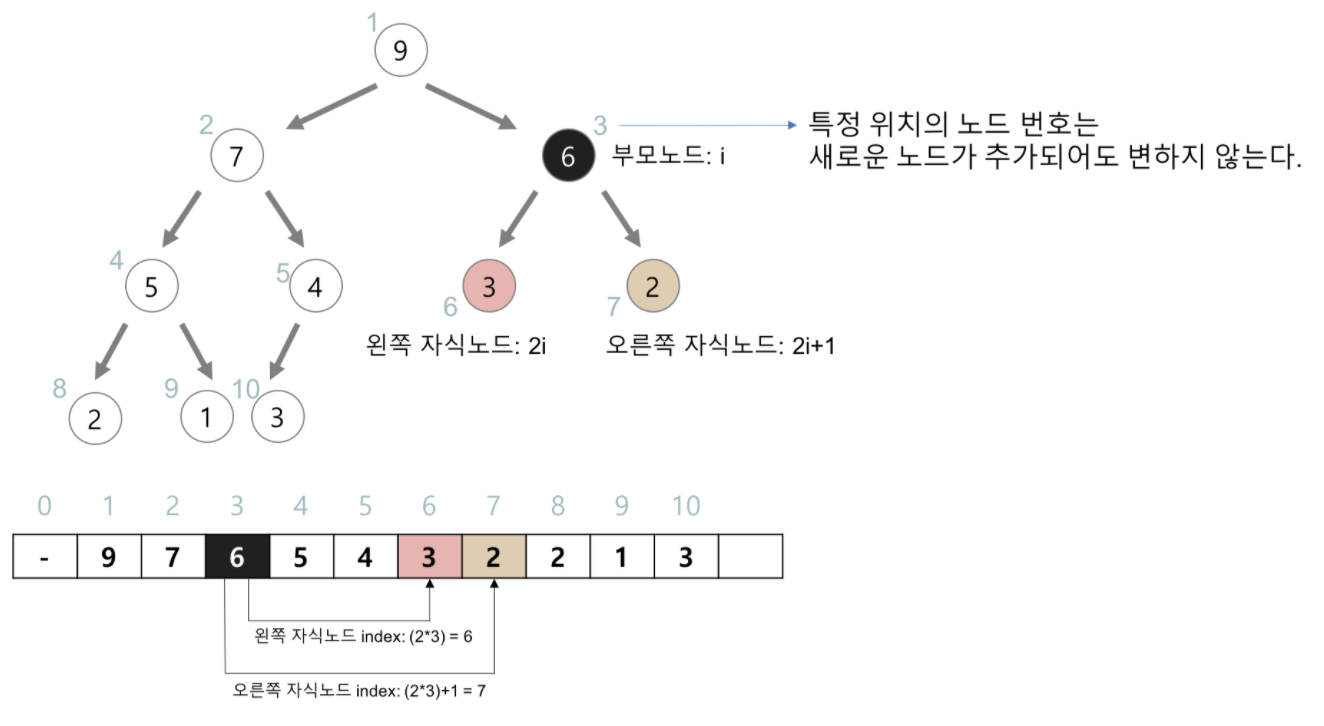
배열의 index로 트리를 살펴보면 위 사진과 같습니다. 배열의 index는 변하지 않고, 그 노드의 value가 변하는 거죠. Heap에서의 부모노드와 자식노드의 관계는 다음과 같습니다.
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
Heap의 삽입

1️⃣ 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입합니다.
2️⃣ 새로운 노드를 부모 노드들과 비교하며 교환해서 힙의 성질을 만족시킵니다.

Heap의 삭제
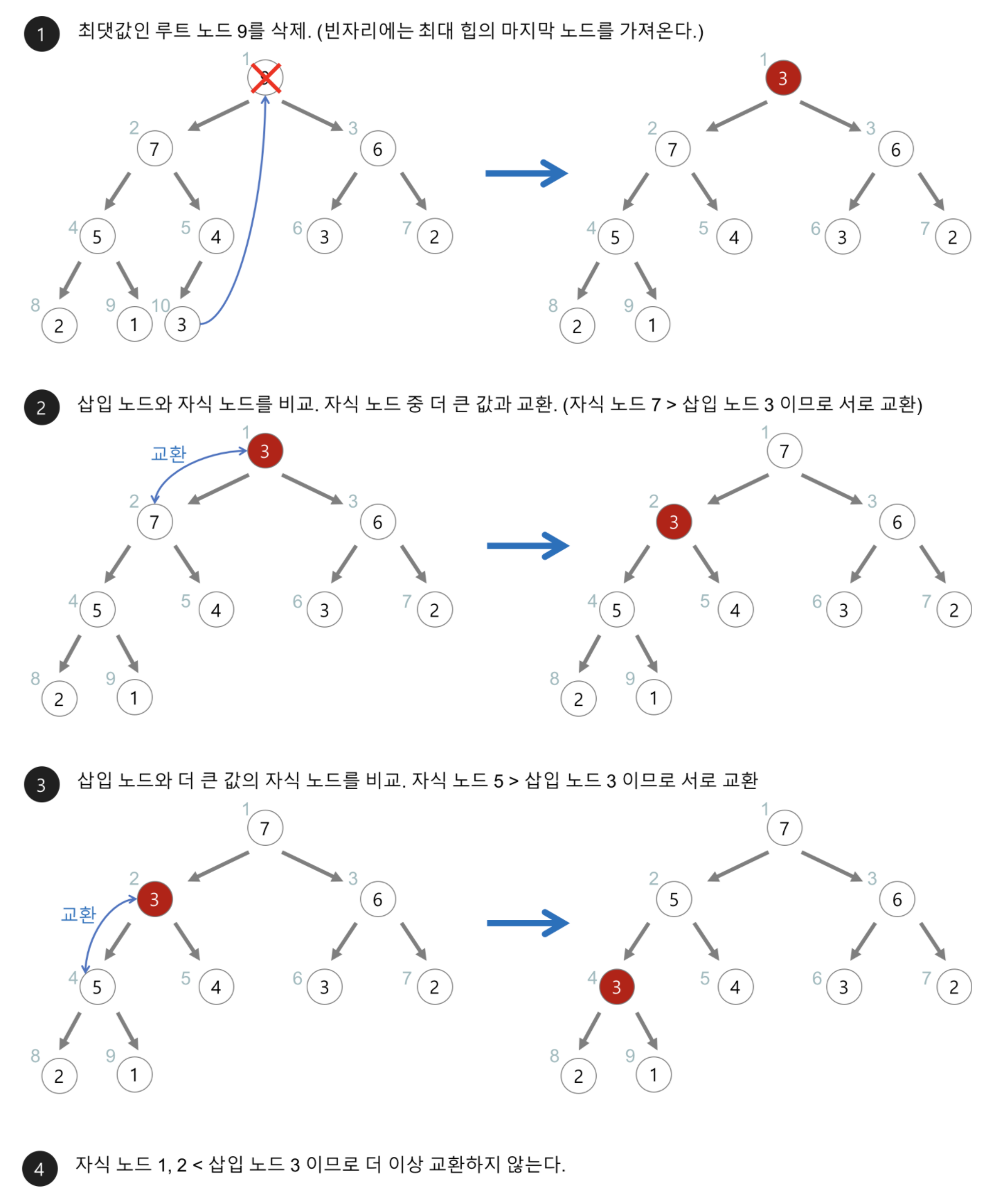
1️⃣ 최대 힙에서의 최댓값은 루트 노드이므로 루트 노드가 삭제됩니다. (Priority Queue 에서 pop 하듯이)
2️⃣ 삭제된 루트 노드에는 힙의 마지막 노드를 가져옵니다.
3️⃣ 힙을 재구성합니다.
1️⃣ 루트 노드와 자식 노드를 비교하여 자식 노드 중 더 큰 값과 교환합니다.
2️⃣ 자식 노드가 루트 노드보다 크다면 계속 반복합니다.
[자료구조] 힙(heap)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
'알고리즘 > 알고리즘&자료구조' 카테고리의 다른 글
| Linked List (링크드리스트) (0) | 2021.02.24 |
|---|---|
| PriorityQueue (우선순위 큐) (1) | 2021.02.19 |
| Insertion Sort (삽입 정렬) (0) | 2021.02.15 |
| Quick Sort (퀵 소트) (0) | 2021.02.12 |
| Merge Sort (병합 정렬) (0) | 2021.02.11 |




댓글